Загадки простых чисел (третья серия). Решето Эратосфена

До сих пор не существует ни одного алгоритма P-класса для решения второй задачи — разложения на простые множители.

Большинство специалистов сходятся во мнении, что такого алгоритма не существует, но в последнее время их уверенность несколько поколебалась. Поскольку где-то за кулисами, совсем рядом, могут скрываться и другие открытия, подобные тесту Агравала-Каяла-Саксены и основанные на таких же простых идеях, как полиномиальная версия теоремы Ферма (и не важно, что пока о них никто даже не подозревает), может оказаться, что системы шифрования, основанные на разложении числа на простые множители, не настолько надежны, как нам хочется верить. Так что пока не стоит раскрывать в Интернете кличку вашей кошки!

Как простые числа распределены среди всех целых чисел?

Даже элементарная математика простых чисел ведет к выдвижению более сложных концепций. Евклид доказал, что простые числа уходят в бесконечность, так что невозможно просто перечислить их все и успокоиться. Мы не можем также дать простую и практичную алгебраическую формулу для вычисления всех простых чисел подряд, примерно так, как по формуле х² вычисляются квадраты чисел.

(Простые формулы существуют, но они «мошенничают», встраивая в формулу сами простые числа под разными личинами, и в результате не сообщают нам ничего нового.) Пытаясь познать природу этих неуловимых и странных чисел, мы экспериментируем, ищем в них признаки структурированности и пытаемся доказать, что найденные нами закономерности присутствуют во всех простых числах, какими бы большими они ни были. Можно, к примеру, задаться вопросом о том, как простые числа распределены среди всех целых чисел. Таблицы простых чисел позволяют предположить, что чем дальше, тем таких чисел становится меньше. В таблице 1 показано, сколько простых чисел содержится в разных диапазонах на 1000последовательных целых чисел.

Таблица 1. Количество простых чисел в последовательных интервалах по 1000 чисел

Интервал	Количество простых чисел
1-1000	168
1001-2000	135
2001-3000	127
3001-4000	119
4001-5000	118
5001-6000	114
6001-7000	117
7001-8000	106
8001-9000	110
9001-10 000	111

Числа во второй колонке по большей части уменьшаются сверху вниз, хотя иногда ненадолго изменяют свое поведение: к примеру, после 114 мы видим 117. Это симптом нерегулярности простых чисел, но в целом общая тенденция прослеживается достаточно четко: чем больше числа, тем реже среди них встречаются простые. За объяснением не нужно далеко ходить: чем больше становится число, тем больше у него потенциальных делителей. А простые числа должны избегать каких бы то ни было делителей. Это напоминает ловлю составных (непростых) чисел рыболовной сетью: чем гуще становится сеть, тем меньшему числу простых чисел удается сквозь нее проскользнуть.

Решето Эратосфена

У этой «сети» есть даже название: решето Эратосфена. Эратосфен Киренский — древнегреческий математик, живший около 276-194 гг. до н.э. Он также был атлетом, интересовался поэзией, географией, астрономией и музыкой.

Как узнать размер Земли?

Эратосфен первым сумел разумным образом оценить размеры Земли, обратив внимание на положение солнца в полдень в двух разных местах — Александрии и Сиене (современный Асуан). В Сиене солнце в полдень стояло точно над головой, а в Александрии отстояло от вертикали примерно на 7°. Поскольку угол в 7° составляет одну пятидесятую часть круга, то и окружность Земли должна в 50 раз превосходить расстояние от Александрии до Сиены.

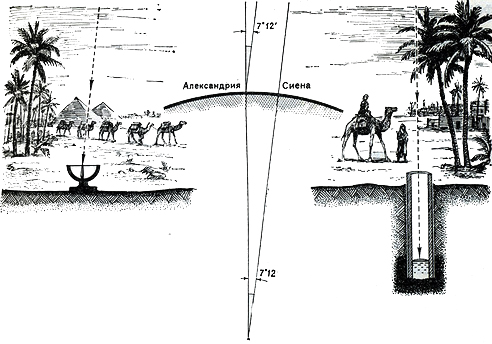
Эратосфен не мог непосредственно измерить это расстояние, поэтому он спросил у караванщиков, сколько времени занимает путешествие на верблюдах из одного города в другой, и оценил, сколько в среднем проходят верблюды за день. Результат своих расчетов он привел в тогдашних единицах расстояния — стадиях, но мы не знаем, чему равнялась стадия. Историки сходятся во мнении, что оценка Эратосфена оказалась достаточно точной.

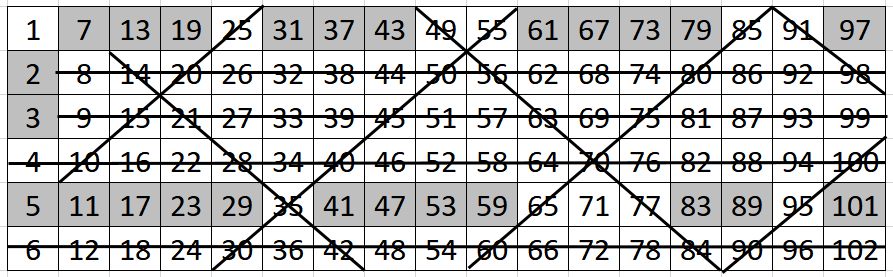
Решето Эратосфена представляет собой алгоритм поиска всех простых чисел путем последовательного исключения из числового ряда чисел, кратных уже известным простым. Рисунок 1 иллюстрирует этот метод на числах от 1 до 102, организованных так, чтобы процесс исключения кратных чисел был хорошо виден. Чтобы посмотреть, как все происходит, я советую вам составить эту или подобную ей схему самостоятельно, с нуля. Для начала начертите табличку и заполните ее числами, ничего не закрашивая и не перечеркивая. Затем потихоньку начинайте вычеркивать. Исключите 1, потому что это единица. Следующее число — 2, оно простое. Вычеркните все числа, кратные 2: это те, что лежат на горизонталях, начинающихся с чисел 4, 6 и 8. Следующее невычеркнутое число — 3, следовательно, оно простое. Вычеркните все числа, кратные 3: это горизонтальный ряд, начинающийся с 6(уже вычеркнут) и с 9. Следующее невычеркнутое число — 5, оно простое. Вычеркиваем все числа, кратные 5: они находятся на диагональных линиях, идущих слева снизу вверх направо и начинающихся на 10, 30, 60 и 90. Следующее невычеркнутое число — 7, оно простое. Вычеркиваем все числа, кратные 7: это диагонали, проходящие сверху слева вниз направо и начинающиеся на 14, 49 и 91. Затем 11 — оно не вычеркнуто, и это простое число. Первое число, кратное 11 и до сих пор не вычеркнутое (т. е. не имеющее меньших делителей) — 121, — находится за пределами нашей таблички. Процесс окончен. Оставшиеся числа в серых ячейках и есть искомые простые числа.

Решето Эратосфена — не просто историческая диковинка, это и сегодня один из наиболее эффективных методов составления длинных списков простых чисел. А родственные ему методы позволили достичь значительного прогресса в решении самой знаменитой, наверное, из великих нерешенных проблем, имеющих отношение к простым числам: проблемы Гольдбаха.

(продолжение следует)

Литература
Иэн Стюард «Величайшие математические задачи».
Материалы Википедии.