Загадки простых чисел (четвертая серия). Проблема Гольдбаха

Загадки простых чисел (четвертая серия). Проблема Гольдбаха

Кристиан Гольдбах переписывался со многими знаменитостями своего времени. В 1742 г. в письме к Леонарду Эйлеру он изложил несколько любопытных гипотез, связанных с простыми числами. Позже историки заметили, что Рене Декарт ранее писал примерно то же самое. Первое из утверждений Гольдбаха звучало так: «Всякое целое число, которое можно представить как сумму двух простых, можно записать также как сумму произвольного числа простых, пока все слагаемые не станут единицами». Второе утверждение, добавленное уже на полях письма, гласило: «Всякое целое число больше двух можно представить как сумму трех простых».

«Всякое целое число больше двух можно представить как сумму трех простых».

Сегодняшнее определение простого числа предполагает очевидные исключения из обоих утверждений. Так, 4 не есть сумма трех простых, поскольку наименьшее простое число — 2, и сумма трех простых не может быть меньше 6. Однако во времена Гольдбаха число 1 считалось простым. Разумеется, его утверждения можно переформулировать в соответствии с современными представлениями.

В ответном письме Эйлер припомнил предыдущий разговор с Гольдбахом, когда тот указал, что первое его заявление является следствием более простой, третьей гипотезы: «Всякое четное целое есть сумма двух простых». С учетом общепринятого представления о 1как о простом числе из этого утверждения прямо следует вторая гипотеза, поскольку любое число можно выразить как n + 1 или n + 2, где n — четное. Если n есть сумма двух простых, то исходное число есть сумма трех простых. Мнение Эйлера о третьем заявлении было однозначным: «Я считаю, что это, несомненно, верная теорема, хотя и не могу ее доказать». Собственно, на сегодняшний день статус этой гипотезы практически не изменился.

«Я считаю, что это, несомненно, верная теорема, хотя и не могу ее доказать».

Современный подход, при котором 1 — не целое число, разбивает гипотезу Гольдбаха на две части. Вариант для четных чисел (так называемая бинарная проблема Гольдбаха) гласит: любое четное целое число больше двух можно представить в виде суммы двух простых чисел.

А вот вариант для нечетных (известный как тернарная проблема Гольдбаха): любое нечетное число больше 5 можно представить в виде суммы трех простых чисел.

Проблема Гольдбаха остается нерешенной уже более 250 ле

Из бинарной гипотезы автоматически следует тернарная, но не наоборот. Есть смысл рассматривать эти гипотезы по отдельности. Тернарная проблема немного проще и в 2013 году она была доказана Харальдом Гельфготтом.

Бинарную гипотезу Гольдбаха для малых чисел можно подтвердить несложными вычислениями:

4 = 2 + 2;

6 = 3 + 3;

8 = 5 + 3;

10 = 7 + 3 = 5 + 5;

12 = 7 + 5;

14 = 11 + 3 = 7 + 7;

16 = 13 + 3 = 11 + 5;

18 = 13 + 5 = 11 + 7;

20 = 17 + 3 = 13 + 7.

Несложно продолжить ряд примеров вручную, скажем, до 1000или около того, а можно и дальше, если хватит терпения. К примеру,
1000 = 3 + 997, а 1000000 = 17 + 999 983. В 1938 г. Нильс Пиппинг проверил бинарную гипотезу Гольдбаха для всех четных чисел вплоть до 100 000.

При этом выявилась общая тенденция: чем больше само число, тем больше способов представить его в виде суммы простых. Это отвечает здравому смыслу. Если вы возьмете большое четное число и начнете вычитать из него по очереди простые числа, с какой вероятностью все результаты этих действий окажутся составными? Достаточно в списке разностей появиться хотя бы одному простому числу, — и можно считать, что гипотеза для исходного числа подтверждена. Обратившись к статистическим свойствам простых чисел, можно оценить вероятность такого исхода. Т 1923 г. аналитики Харольд Харди и Джон Литлвуд проделали такую операцию и вывели правдоподобную, но нестрогую формулу для числа способов представления заданного четного n в виде суммы двух простых чисел: это число приблизительно равно n/(2(ln п)²). Это число увеличивается с ростом n и, кроме того, хорошо согласуется с числовыми данными. Но даже если математикам удалось бы сделать эту формулу точной, невозможно было бы исключить возможность того, что из нее существуют очень редкие, но все же исключения, так что формула не слишком помогает.

Основное препятствие: простые числа определяются через умножение, а в самой гипотезе речь идет о сложении.

Основное препятствие, мешающее доказать гипотезу Гольдбаха, заключается в том, что она сочетает в себе две очень разные характеристики. Простые числа определяются через умножение, а в самой гипотезе речь идет о сложении. Поэтому необычайно трудно соотнести желаемый вывод с каким бы то ни было разумным свойством простых чисел. Такое впечатление, что рычаг просто некуда вставить. Должно быть, эти слова звучали настоящей музыкой в ушах владельцев изда­тельства Faber&Faber, когда в 2000 г. они пообещали премию в 1000000 долларов за доказательство гипотезы. Сделано это было ради продвижения романа Апостолоса Доксиадиса «Дядя Петрос и проблема Гольдбаха». Сроки поджимали: решение необходимо было представить до апреля 2002 г. Премия эта так никому и не досталась, что едва ли удивительно, если учесть, что проблема Гольдбаха остается нерешенной уже более 250 лет.

Гипотезу Гольдбаха часто формулируют иначе — как вопрос о сложении множеств целых чисел. Бинарная проблема Гольдбаха — простейший пример такого подхода, поскольку при этом мы складываем всего лишь два множества. Для этого нужно взять любое число из первого множества, добавить к нему любое число из второго и составить из всех таких сумм свое, третье множество. Так, сумма множеств {1, 2, 3} и {4, 5} содержит 1 + 4, 2 + 4, 3 + 4,1 + 5, 2+ 5, 3 + 5, т. е. {5, 6, 7, 8}. Некоторые числа возникают здесь не по одному разу; к примеру, 6= 2 + 4 = 1 + 5. Называются подобные повторы перекрытием.

Если сложить множество простых чисел с самим собой, то полученное в результате множество будет содер­жать все четные числа больше двух.

Теперь можно сформулировать бинарную гипотезу Гольдбаха заново: если сложить множество простых чисел с самим собой, то полученное в результате множество будет содер­жать все четные числа больше двух. Такое изменение формулировки может показаться немного банальным — так оно, кстати, и есть, — но оно помогает переместить проблему в ту область математики, где есть некоторые убедительные теоремы общего характера. Немного мешает число 2, но от него можно без труда избавиться. 2 — единственное целое простое число, и при сложении его с любым другим простым числом результат получается нечетный. Так что во всем, что касается гипотезы Гольдбаха, о двойке можно просто забыть. Однако 2 + 2нам потребуется для представления числа 4, поэтому нам придется ограничить свое внимание четными числами начиная с 6.

В качестве эксперимента рассмотрим простые числа до 30 включительно. Таких чисел девять: {3, 5, 7, 11, 13, 17, 19, 23, 29}. При сложении этого множества с самим собой получится то, что можно увидеть на рис. 1: я выделил суммы, меньшие или равные 30 (диапазон четных чисел, в который укладыва­ются все простые до 29) жирным шрифтом. При таком представлении результата ясно видны две простые закономерности. Во-первых, вся таблица симметрична относительно главной диагонали, поскольку а + b = b + а. И, во-вторых, выделенные числа занимают приблизительно левую верхнюю половину таблицы (см. рис. 1) над жирной (проходящей по диагонали) линией. Мало того, в середине они даже норовят вылезти за нее. Происходит это потому, что в среднем большие про­стые числа встречаются реже, чем маленькие. Дополнитель­ная выпуклость посередине с лихвой компенсирует числа 32 в верхнем правом и нижнем левом углах.

Теперь мы можем сделать некоторые грубые оценки. Чис­ло ячеек в таблице составляет 9 х 9 = 81. Около половины чисел в этих ячейках находятся в левом верхнем треугольнике. Благодаря симметрии все числа, кроме лежащих на диагонали, имеют симметричную пару, так что число независимых ячеек составляет примерно 81/4, т. е., округляя, 20. В интервале от 6до 30 содержится 13 четных чисел, поэтому 20 (и даже боль­ше) выделенных чисел могут принимать лишь 13 четных значе­ний. Это значит, что в данном диапазоне потенциальных сумм двух простых больше, чем четных чисел. Представьте, что вы на ярмарке и вам нужно 20 мячиками поразить 13 мишеней. Согласитесь, что шанс попасть в большую часть из них у вас будет неплохой. Тем не менее по нескольким вы можете и про­мазать. Иными словами, не исключено, что некоторых четных чисел все же будет не хватать.

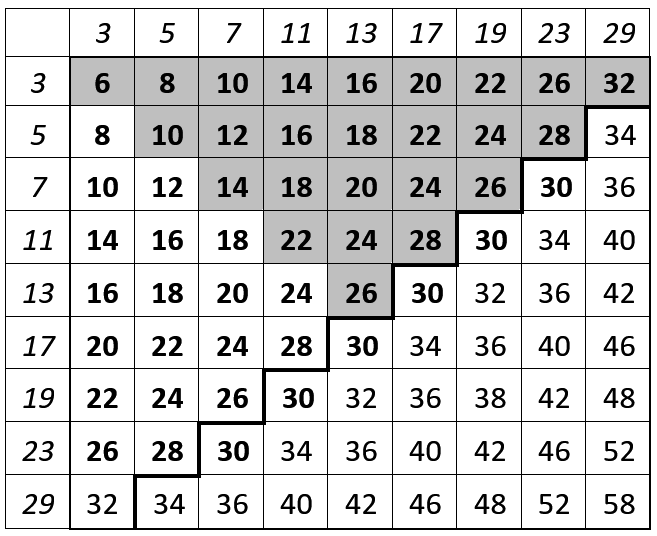
В данном случае все числа на месте, но практические аргу­менты такого рода не позволяют полностью исключить подоб­ную возможность. Однако из этого примера видно, что пере­крытий должно быть немало: ведь одни и те же выделенные числа встречаются в интересующей нас четверти таблицы по несколько раз. Почему? Потому что 20 сумм должны уложиться в множество, где всего 13 членов. Поэтому каждое выделенное число в среднем встречается в таблице 1,5 раза. (Реальное количество сумм — 27, и более точная оценка показывает, что каждое выделенное число встречается дважды.) Если же каких-то четных чисел в таблице не хватает, то пере­крытие должно быть еще больше.

Можно сыграть в ту же игру в более широком диапазоне, с более высоким верхним пределом — скажем, до одного миллиона. Формула, известная как теорема о распределении про­стых чисел, дает нам возможность подсчитать количество простых чисел в интервале до любого заданного числа х. Эта оценка — x/ln х. В интервале до 1000000 количество простых оценивается по этой формуле в 72 380. (Точное их число 78 497.) Серый фон занимает около четверти соответствующей таблицы, поэтому в нем примерно n²/4 = 250 млрд выделенных чисел — столько в этом диапазоне возможных сумм двух простых. Это намного больше, чем количество четных чисел в этом же диапазоне (их полмиллиона). Теперь перекрытие должно быть гигантским, а суммы должны возникать в среднем по 500000 раз каждая. Так что шанс на то, что какое-то четное число окажется пропущено, многократно снижается.

Приложив еще некоторые усилия, мы можем с помощью этого метода оценить вероятность того, что некое четное число в заданном диапазоне не окажется суммой двух простых, исходя из того, что простые числа распределяются случайно с периодичностью, описываемой теоремой о распределении простых чисел, т. е. что в диапазоне до любого заданного х находится около x/ln х простых чисел. Именно это сделали Харди и Литлвуд. Они понимали, что такой подход не является строгим, поскольку простые числа определяются достаточно специфически и распределены на самом деле не случайно. Тем не менее разумно ожидать, что реальные результа­ты не войдут в противоречие с этой вероятностной моделью, поскольку определяющее свойство простых чисел, судя по все­му, очень слабо связано с тем, что происходит при сложении двух таких чисел.

Несколько стандартных методов в этой области математики используют примерно такой же подход, но стараются дополнительными средствами сделать свою аргументацию как можно более строгой.

(продолжение следует)

Литература
Иэн Стюард «Величайшие математические задачи».
Материалы Википедии.