Олимпиадная классика (7)

Олимпиадная классика (7)

Написанное на доске четырехзначное число можно заменить на другое, прибавив к двум его соседним цифрам по единице, если ни одна из этих цифр не равна 9, либо вычтя из соседних двух цифр по единице, если ни одна из них не равна 0. Можно ли с помощью таких операций из числа 1234 получить число 2002?

Решение. Пусть на доске написано число

Тогда рассматриваемые операции не изменяют число М = (d + b) – (а + с), так как они увеличивают (уменьшают) на единицу одно число из первой скобки и одно число из второй. Для числа 1234 число М₁ = (4 + 2) – (1 + 3) = 2, для числа 2002 число М₂ = (2 + 0) – (2 + 0) = 0. Поэтому требуемое невозможно.

Ответ. Нельзя.

В каждой клетке доски 7×7 сидит жук. В какой-то момент времени все жуки взлетают, и после этого каждый из жуков садится в клетку, соседнюю по стороне с той, из которой он взлетел. Докажите, что в какую-то клетку не сядет ни одного жука.

Решение. Рассмотрим шахматную раскраску доски в черный и белый цвета. Тогда у нас 25 клеток покраше­но в черный цвет, а 24 — в белый. Заметим, что жук, взлетевший с белой клетки, сядет на черную клетку, а взлетевший с черной — на белую. Но с белых клеток взлетают 24 жука, и они не смогут сесть на 25 клеток.

На доске написаны числа 1, 2 и 4. Разрешается стереть с доски два числа а и b, а вместо них записать числа

 Можно ли с помощью таких операций получить на доске числа

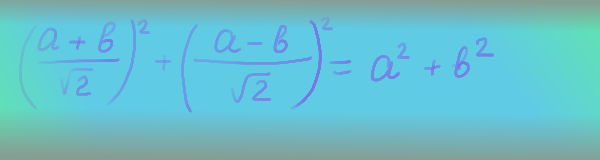
Решение. Заметим, что при данной операции не меняется сумма квадратов чисел, записанных на доске:

Но у начальной тройки чисел сумма квадратов рав­на 21, а у той, которую мы хотим получить, сумма квадратов равна 19. Поэтому указанную тройку получить нельзя.

Ответ. Нельзя.