Олимпиадная классика (6)

Каково наименьшее натуральное n, такое, что n! делится на 18, на 19, на 20 и на 21?

Решение. Заметим, что число 19 простое, поэтому если n < 19, то n! не делится на 19. Осталось понять, что 19! делится и на 18, и на 19, и на 20 (20 = 5 × 4), и на 21 (21 = 7 × 3).

Ответ. 19.

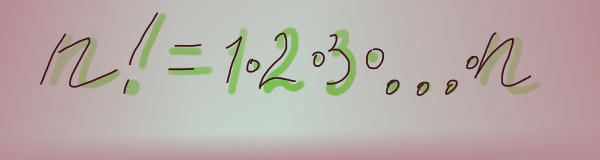
Несколько камней весят вместе 10 т, при этом каждый из них весит не более 1 т. На каком наименьшем количестве трехтонок можно увезти этот груз за один раз?

Решение. Покажем, что на пяти трехтонках можно увезти весь груз за один раз. Действительно, на каждой из четырех первых трехтонок можно увезти более 2 т камней, т. е. первые 4 машины увезут по крайней мере 8 т камней. Оставшиеся камни (суммарным весом менее 2 т) увезет пятая машина. Покажем теперь, что четырех машин может не хватить. Действительно, если бы изначально было 13 камней весом по 10/13 т каждый, то одна трехтонка увезла бы только 3 таких камня, т. е. 4 трехтонки могут увезти лишь 12 из 13 камней.

Ответ. На пяти трехтонках.

В турнире по олимпийской системе (проигравший выбывает) участвуют 50 боксеров. Какое наименьшее количество боев надо провести, чтобы выявить победителя?

Решение. После каждого боя из соревнований выбывает один боксер, проигравший в этом бою. Поскольку всего к концу соревнований выбыть должны все, кроме победителя, всего должно быть 49 боев независимо от того, как составляется расписание.

Ответ. 49.