Олимпиадная классика (2)
Десятичная запись числа А состоит из 30 единиц и нескольких нулей. Может ли число А быть полным квадратом?
Решение. Сумма цифр числа А равна 30. Поэтому оно делится на 3, но не делится на 9, т. е. оно не может быть полным квадратом.
Ответ. Не может.

Дети, построенные парами, выходят из лесу, где они собирали орехи. В каждой паре идут мальчик и девочка, причем у мальчика орехов либо вдвое больше, либо вдвое меньше, чем у девочки. Могло ли так случиться, что у всех вместе 1000 орехов?
Решение. Заметим, что число орехов у каждой пары детей делится на 3. Это означает, что суммарное число орехов должно делиться на 3. Однако 1000 на 3 не делится.
Ответ. Не могло.
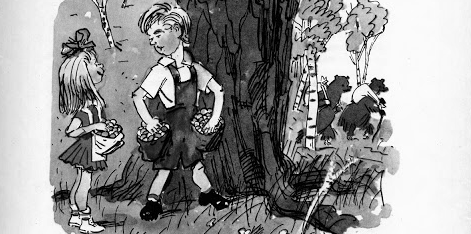
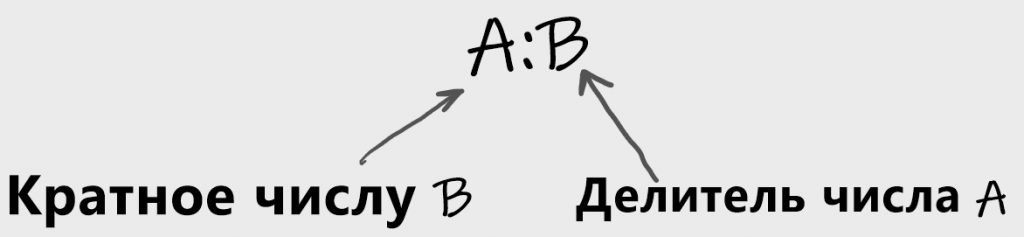
Докажите, что число имеет нечетное число делителей (включая единицу и само число) тогда и только тогда, когда оно является точным квадратом.
Решение. Пусть нам дано число S и а — его делитель. Тогда число S/a также является делителем числа S, т. е. делители числа разбиваются на пары. У числа может быть нечетное число делителей, только если числа в какой-нибудь паре совпадают: S/a = а, откуда S = а2. И наоборот, если S = а2, то S/a = а, т. е. у числа будет нечетное число делителей.
Литература.
Агаханов Н.Х. Математика. Районные олимпиады
